Что такое граф?
Геометрическое представление графа
Способы представления графа в памяти компьютера

Что такое граф?

Графом называется пара (V,E), где V - конечное множество вершин, а E - набор неупорядоченных и упорядоченных пар вершин. Обозначим граф G=(V,E). Неупорядоченная пара вершин называется ребром, упорядоченная - дугой. Граф содержащий только ребра называется неориентированным, только дуги - ориентированным, или орграфом.

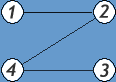
Если вершины v и u соединены ребром e, то говорят, что они смежны между собой, а ребро e инцидентно каждой из них. Количество ребер графа, инцидентных вершине v называется степенью данной вершины. Для ориентированного графа выделяют входящую степень, равную количеству входящих ребер и исходящую степень, равную количеству исходящих ребер, а степенью вершины в таком случае называют сумму ее входящей и исходящей степени. Вершины имеющие степень 0 называют изолированными.

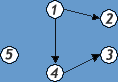
Для орграфа на рис.3 входящие степени вершин 1,2,3,4,5 равны соответственно 0,1,1,1,0, исходящие - 2,0,0,1,0. Степени вершин, получаемые сложением входящих и исходящих степеней равны 2,1,1,2,0. Таким образов, вершина 5 - изолированная.

Ребро, соединяющее вершину саму с собой называется петлей. Если одну пару вершин соединяют два или более ребер, то такие ребра называют кратными. Граф называется простым, если он не содержит ни петель, ни кратных ребер, иначе граф называется мультиграфом. (В некоторых источниках граф с кратными ребрами называют мультиграфом, с петлями - псевдографом.) Простой граф, любая пара вершин которого соединена ребром, называется полным. В полном графе n*(n-1)/2 ребер.

Граф называется разреженным, если общее количество ребер значительно меньше их возможного количества. Иначе граф называется плотным.

Подграфом графа G=(V,E) называется граф G'=(V',E') такой, что V'⊆V, E'⊆E.

Путем из вершины u в вершину x называется последовательность вершин (v₀,v₁,...,v_k), в которой v₀=u, v_k=x и (v_i-1,v_i) ∈ E. Длина этого пути равна k. Такой путь проходит через вершины v₀,v₁,...,v_k, а также ребра (v₀,v₁), (v₁,v₂),...,(v_k-1,v_k). Вершина v₀ - начало пути, v_k - конец пути. Говорят, что путь ведет из v₀ в v_k. Если существует путь из вершины u в вершину x, говорят, что x достижима из u.

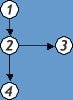
Пример. На рис.4 последовательность вершин (5,1,3,4) является путем.

Путь называется простым, если он содержит каждую из вершин не более одного раза.

Неориентированный граф называется связным, если существует хотя бы один путь между каждой парой вершин, и несвязным в противоположном случае.

Ориентированный граф связен, если связен неориентированный граф, получаемый из этого орграфа снятием ориентации с дуг. Ориентированный граф сильно связен, если для любой пары вершин v и u существут путь из v в u и из u в v.

Связной компонентой графа называется максимальный связный подграф этого графа. Сильно связной компонентой называется максимальный сильно связный подграф.

Циклом называется путь из некоторой вершины в эту же вершину, содержащий хотя бы одно ребро. Цикл простой, если в нем нет повторяющихся вершин (за исключением начальной (конечной), которая является первой и последней вершиной пути).

Граф, в котором нет циклов называется ациклическим.

Связный граф без циклов называется деревом.

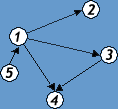
Граф называется двудольным, если множество его вершин V можно разбить на непересекающиеся подмножества V₁ и V₂ так, что никакие две вершины одного подмножества не смежны. Пример двудольного графа на рис. 5.

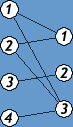
Графы G₁=(V₁,E₁) и G₂=(V₂,E₂) изоморфны, если существует такое взаимно однозначное отображение ƒ:V₁→V₂, что для произвольных v и u∈V₁ имеем (v,u)∈E₁⇔(ƒ(v),ƒ(u))∈E₂. Отображение ƒ называется изоморфизмом (или изоморфным отображением) графов G₁ и G₂. При изоморфизме каждая вершина переходит в вершину с той же степенью. Пример изоморфных графов на рис.6 (1->2, 2->4, 3->5, 4->3, 5->1).

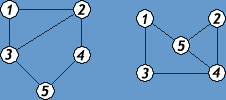
Геометрическое представление графа

Любой граф можно представить множеством точек на плоскости, соответствующих вершинам, соединенных линиями, соответствующими ребрам. В трехмерном пространстве граф всегда можно представить таким образом, что эти линии не будут пересекаться.

Способы представления графа в памяти компьютера

При разработке эффективных алгоритмов выбор структуры данных имеет принципиальное значение. Рассмотрим три основных структуры.

Список ребер

Наиболее очевидный способ - хранить список пар вершин, соединенных ребрами. Для его хранения необходим двумерный массив размерности Mx2 (M - количество ребер). Строка массива описывает ребро. Для взвешенных графов такой способ создает необходимость дополнительно завести массив весов ребер.

Пример для орграфа на рис.4:

	e1	e2	e3	e4	e5
v1	5	1	1	3	1
v2	1	2	3	4	4

Матрица смежности.

Матрица смежности A представляет собой двумерный массив размерности NxN (N - количество вершин). A[i,j]=1, если существует ребро (i,j) (дуга <i,j>), A[i,j]=0 - в противном случае. Для неориентированных графов матрица смежности симметрична относительно главной диагонали.

Для взвешенных графов значение элемента A[i,j] обычно используют для хранения веса соответствующего ребра. Для невзвешенных мультиграфов A[i,j] может содержать количество ребер, соединяющих вершины i и j.

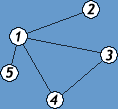
Пример. Матрица смежности для графа на рис.7:

	v1	v2	v3	v4	v5
v1	0	1	1	1	1
v2	1	0	0	0	0
v3	1	0	0	1	0
v4	1	0	1	0	0
v5	1	0	0	0	0

Список связей

Третий способ - хранение списка всех ребер инцидентных каждой из вершин. Для этого необходим массив, содержащий N элементов, где N - количество вершин в графе. i-ый элемент этого массива содержит список всех ребер, смежных с i-ой вершиной (ребро представлено номером второй инцидентной ему вершины).

Пример для графа на рис. 7.

Вершина	Смежные вершины
1	2,3,4,5
2	1
3	1,4
4	1,3
5	1

Итого:

Пусть N и M - количество элементов в множествах V и E соответственно, d_max - максимальная степень вершины, тогда сравнительную характеристику вышеназванных структур удобно представить в виде таблицы:

	Список ребер	Матрица смежности	Список связей
Память	2*M	N2	2*M
Проверка смежности двух вершин	M	1	dmax
Получение списка всех вершин, смежных данной	M	N	dmax
Добавление ребра	1	1	1
Удаление ребра	M	2	2*dmax